We have developed a new model for Benford’s Law analysis.
You can analyze naturally occurring numbers (e.g. transaction level data) to see if the actual distributions conform to Benford’s Law. Under certain conditions, deviations from Benford’s could indicate the possibility of human manipulation, i.e. fraud. Therefore, those results would require additional scrutiny. This analysis provides a direction of inquiry.
This is a model for Benford’s Law analysis built in MS Excel which calculates graphical and tabular results for the following tests:
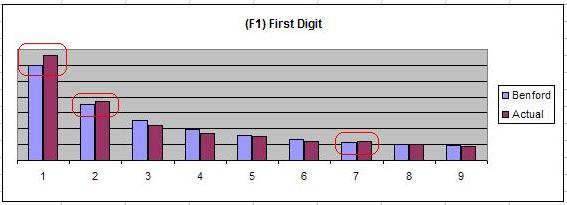
(F1) First Digit
(D2) Second Digit
(F2) First Two Digits
(F3) First Three Digits
(L1) Last Digit
(L2) Last Two Digits
— Raw statistics on the data are calculated such as: N, Min, Max, Md, Mode, Mean, & StdDev. In addition, the model will automatically indicate if there is a relationship between the data set and Benford’s, e.g. “The actual data conforms to a Benford’s distribution.” Otherwise, the analysis would not be meaningful and the construction of the data set would need to be reconsidered.
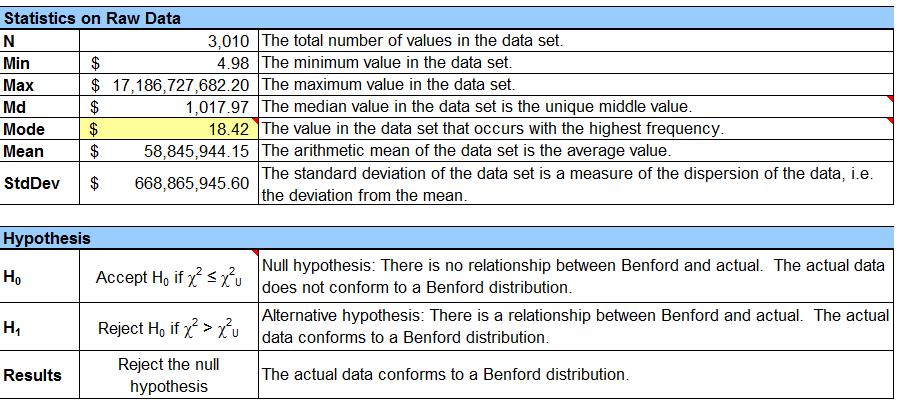
— Calculations to determine if the data set is large enough are performed. The Chi-Square statistical test for independence is calculated and automatically indicates if the data set is large enough to analyze, e.g. “All frequencies meet the requirement.” The default confidence interval for level of significance is set at 95%, however it can easily be changed by the drop down highlighted in yellow below.

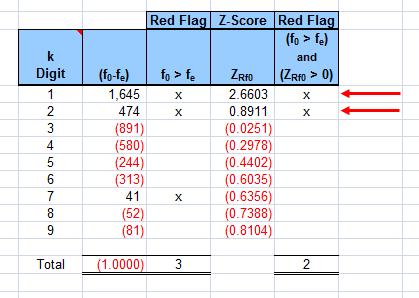
— Z-Scores are calculated for each digit as a measure of risk. The red flag is highlighted when the count (frequency) of actual (observed) data is greater than Benford’s (expected) and the Z-Score percentage (relative frequency) is positive (greater than zero): [frequency(observed) > frequency(expected)] and [Z-Score(relative frequency of the observed) > zero]
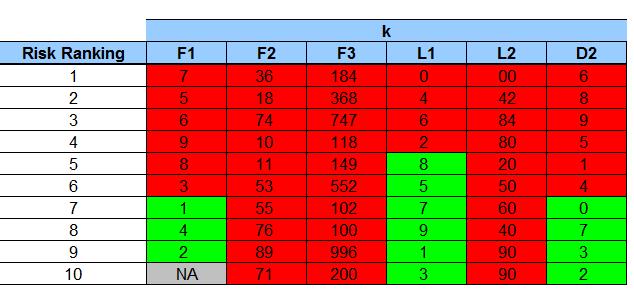
— Risk for each digit is rank ordered for all tests. The top ten risks by digit (k) for each test (F1, F2,f 3, L1, L2, D2) are rank ordered and color coordinated to create a heatmap for risk.
— Step by step instructions and interpretations are included in the “User Notes” tab.
For this and other tools, go to: Antifraud Tools
